UMAPは、高次元データの次元を低次元に削減する手法の一つです。
本記事では、Pyhtonを使ってUMAPで次元削減する方法や、クラスタリングへの活用方法などを解説しています。
この記事を読んで、UMAPをどのように活用するかの参考にしてください。
PHPを独学で勉強した後にWeb業界に参入。大手企業でプログラマーとして活躍後、自社サービスの立ち上げ、大手検索エンジンサービスの保守運用作業、ソーシャルゲーム開発などに携わりながら、SE・管理職の道を歩んで現在に至る。現在は、管理職に携わる傍ら、これまでの経験を活かした執筆活動を続けている。
次元削減手法:UMAPとは?

UMAP(Uniform Manifold Approximation and Projection)は、高次元データの次元を低次元に削減する手法の一つです。次元削減は、データの特徴を維持しながら、視覚化や計算の効率化を目的としています。
ここでは、UMAPのことをよく理解するために、以下の項目に分けてUMAPの詳細を解説します。
- UMAPが解決してくれる問題
- UMAPの歴史的背景
UMAPは、データの局所的な構造を重視し隣接するデータポイント間の距離を維持することで、元のデータの幾何構造を低次元空間に再現します。
UMAPが解決してくれる問題
UMAPは、特に高次元データの次元削減に伴う問題を解決します。
データが高次元になると可視化が困難になり、クラスタリングや分類などの分析が直感的にできなくなる問題が発生しがちです。
UMAPは、データの局所的な構造を保ちながら低次元空間にプロジェクトするため、パターンやクラスターが視覚的に確認しやすくなります。
さらに、UMAPは高次元データにおけるノイズの影響を減らすことができるため、データの本質的な特徴を抽出するのに役立つでしょう。
UMAPの歴史的背景
UMAPは、2018年にLeland McInnesらによって提案された次元削減手法です。
その背景には、高次元データの可視化や解析が重要視される機械学習やデータサイエンスの発展があります。従来からt-SNEなどの非線形次元削減手法が使われていましたが、UMAPはそれらに比べて計算効率が高く、大規模データでも適用可能です。
UMAPの理論はリーマン多様体理論や代数的トポロジーに基づいており、データの局所的な構造を忠実に保ちながら、非線形なデータの関係性を低次元空間で再現します。
UMAPは、多様な分野でのデータ可視化や解析に広く利用されるようになりました。
UMAPの特徴

UMAPは、高次元データの次元を低次元に削減する手法の一つであることがわかりました。では、UMAPの特徴にはどのようなものがあるのでしょうか。
ここでは、以下の項目に分けてUMAPの特徴を解説します。
- 次元削減の処理が非常に速い
- データを分かりやすく可視化できる
- 大規模なデータ分析にも応用できる
UMAPは、次元削減の処理が非常に早い次元削減手法です。
次元を削減することで、データをわかりやすく可視化でき、大規模なデータ分析にも応用できる特徴があります。
次元削減の処理が非常に速い
UMAPの大きな特徴の一つは、次元削減の処理が非常に速いことです。
UMAPは、高次元データを低次元空間に変換する際に、データの局所的な構造を保つためのアルゴリズムを効率的な実行が可能。t-SNEなどの他の非線形次元削減手法と比べても、計算時間が大幅に短縮されます。
データを分かりやすく可視化できる
UMAPのもう一つの特徴は、データを視覚的にわかりやすく可視化できる点です。
UMAPは、高次元空間でのデータポイント間の関係を、低次元空間(通常は2次元や3次元)に投影し、その構造を直感的に示します。
データのクラスタリングやパターンを視覚的に確認できるため、データの分布や類似性を理解しやすいでしょう。
また、UMAPは非線形な関係性も捉えることができ、複雑なデータの潜在的なパターンを発見するのに役立つでしょう。
大規模なデータ分析にも応用できる
UMAPは、大規模なデータ分析にも適用できるスケーラビリティが大きな特徴です。
従来の次元削減手法(例えばt-SNE)は計算コストが高く、データセットが大規模になると実行時間が増大します。
また、UMAPは大規模データにおいても高次元空間の局所的な構造を忠実に保ちながら、低次元空間に再現できるため、ビッグデータやリアルタイムのデータ分析においても優れたパフォーマンスを発揮します。
UMAPは医療、バイオインフォマティクス、マーケティング、金融など、多岐にわたる分野で活用されている技術です。
UMAPの活用例

UMAPは、次元削減の処理が非常に速く、データをわかりやすく可視化できる特徴があることがわかりました。次に、UMAPの活用例をみていきましょう。
ここでは、以下の項目に分けて、UMAPの活用例を紹介します。
- クラスタリングとの組み合わせ
- UMAPを使ったデータの可視化
- UMAPを使った異常検知
- UMAPを使った音声認識
UMAPは、クラスタリングと組み合わせたり、異常検知や音声認識に対する活用例があります。それぞれの項目を見て、どのように活用されているかを理解していきましょう。
クラスタリングとの組み合わせ
UMAPはクラスタリング手法と組み合わせて効果的な活用が可能です。
UMAPで高次元データを低次元に削減することで、データの構造が視覚的に理解しやすくなり、その後のクラスタリング手法の精度や効率が向上します。
UMAPは局所的なデータ構造を保持するため、K-meansではデータが自然に分割され、DBSCANではノイズを含む複雑なクラスタ構造も効果的に検出可能です。
この組み合わせにより、次元削減とクラスタリングの相乗効果が得られ、特に大規模データや非線形なデータに対して有用な分析が可能となります。
以下の記事では、クラスタリングに関して詳しく解説しています。ぜひご一読ください。
UMAPを使ったデータの可視化
UMAPは、2次元や3次元でデータを可視化するための強力なツールとして広く活用されています。
高次元の複雑なデータを、UMAPを用いて低次元に投影することで、データのパターンやクラスタ構造を視覚的に確認することが可能です。
UMAPは、非線形な関係を捉える能力が高く、隠れた構造を可視化するのに適しているため、パターン認識や異常検知、分類問題の前処理としても有用です。
データの傾向を直感的に把握し、探索的データ分析やプレゼンテーションにも役立ちます。
UMAPを使った異常検知
UMAPは異常検知にも有効に活用できます。
UMAPを使って高次元データを低次元空間に投影すれば、異常なデータ点(異常値)が視覚的に目立つようにすることが可能です。
通常、異常値は他のデータと異なる特徴を持つもの。UMAPで低次元に変換されたデータ空間では、異常値が孤立して表示されたり、通常のクラスタとは離れた場所に位置します。
UMAPを活用すれば、異常データを直感的に把握しやすくなり、異常検知の精度が向上するでしょう。
特に、複雑な非線形データや多次元データでの異常検知に有効で、金融データの不正取引検知や医療データの異常パターン発見など、さまざまな応用が可能です。
UMAPを使うことで、データの異常点が明確に可視化され、より効果的な分析が実現します。
UMAPを使った音声認識
UMAPは音声認識分野でも次元削減手法として有効に活用されています。
音声データは時間的な変化や周波数情報など、多くの高次元の特徴を含んでおり、これらを直接処理するのは計算コストが高く複雑です。しかし、UMAPを用いることで高次元の音声データの特徴を低次元に削減し、よりシンプルで効率的に扱えるようになります。
UMAPは、音声データの局所的なパターンや特徴を保ちながら次元削減を行うため、音声信号の特徴抽出や分類に有効です。
話者識別や音声コマンド認識の精度向上に寄与し、音声認識システムのパフォーマンスを最適化することが可能です。
Python環境でUMAPを実装する手順

UMAPは、データの可視化や異常検知など、さまざまな分野で活用されていることがわかりました。次に、Pyhton環境でのUMAPを実装する手順をみていきましょう。
ここでは、以下の項目に分けて、Python環境でUMAPを実装する手順を解説します。
- 必要なライブラリのインポート
- UMAPオブジェクトの作成
- fit_transformメソッドの使用
UMAPは、必要なライブラリをインポートした上で利用する必要があります。手順をよくみながら、UMAPを利用する準備を進めましょう。
以下の記事では、Pythonの活用事例などを詳しく解説しています。ぜひこちらもご覧ください。
必要なライブラリのインポート
Python環境でUMAPを実装するには、まず必要なライブラリをインポートし、データを準備してUMAPで次元削減を行います。
まずは、必要なライブラリのインストールを実施しましょう。UMAPはumap-learnというライブラリに含まれています。
以下のコマンドでインストールします。

次に、実装に必要なライブラリをインポートします。
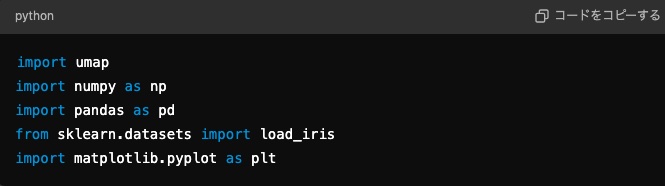
以上で、必要なライブラリのインポートは完了です。
UMAPオブジェクトの作成
UMAPオブジェクトを作成する際、まずは、UMAPのインポートから行います。
以下のコマンドで、UMAPの実装に必要なライブラリumap-learnをインポートしましょう。

UMAPオブジェクトはumap.UMAP()クラスを使って作成します。なお、オブジェクト作成時に、いくつかのパラメータを設定できます。
- n_neighbors: データポイント間の局所的な関係を捉えるための近傍数(デフォルトは15)。
- n_components: 次元削減後の次元数(通常2か3)。
- metric: 距離の計算に使用する指標(デフォルトはユークリッド距離)。
今回は、2次元に削減するUMAPオブジェクトを作成します。

上記コマンドを実行したら、UMAPオブジェクト作成の完了です。
fit_transformメソッドの使用
fit_transformメソッドは、UMAPオブジェクトを用いてデータに次元削減を適用するためのメインメソッドです。このメソッドは、データにフィッティング(適合)しながら、次元削減を実行します。
fit_transformメソッドを使い、UMAPによる次元削減を実行しましょう。このメソッドは、UMAPオブジェクトにデータを渡し、次元削減後のデータを返します。

次元削減後のデータはX_embeddedに保存され、元の高次元データが低次元に変換されます。この結果を用いて可視化やクラスタリングが可能です。
データ前処理とUMAPの適用

PythonでUMAPを簡単な手順で利用できることがわかりました。次に、データ前処理とUMAPの適用がどのようになっているのかみていきましょう。
ここでは、以下の項目に分けて、データ前処理とUMAPの適用を解説します。
- カテゴリデータの処理
- 欠損値の処理
- 外れ値の処理
- 標準化・正規化する
それぞれの項目は、UMAPを利用する際のデータ前処理として必要なものばかりです。一つ一つ理解していきましょう。
カテゴリデータの処理
UMAPを適用する前に、カテゴリデータを適切に処理することは重要です。
UMAPは距離に基づく次元削減手法であり、連続値データの距離を計算するのに適していますが、カテゴリデータ(例: 性別、職業など)はそのままでは使用できません。これを処理せずにUMAPに入力すると、結果が歪むか、意味のない結果となってしまうでしょう。
適切にエンコードされたカテゴリデータは、UMAPの次元削減結果に正しく反映され、同じカテゴリに属するデータ点が近くに配置されます。逆に、未処理のカテゴリデータを使うと、UMAPの結果が不正確になり、誤ったクラスタリングやパターンが示される可能性があるため、データ前処理が必須です。
欠損値の処理
欠損値(NaNやnull)を適切に処理することは、UMAPを適用する前の重要な処理です。
UMAPは数値データを前提とした距離に基づく次元削減手法であり、欠損値が含まれるデータでは計算が行えません。
欠損値をそのままにしてUMAPを適用するとエラーが発生し、正しく実行できないため、事前に処理が必要です。欠損値を適切に処理しないと、UMAPの実行ができません。
また、欠損値の処理方法が結果に大きく影響します。欠損値を削除するとデータ量が減ってパターンが変わる可能性があり、補完した場合は、補完方法によってはUMAPの結果に偏りが生じることがあるでしょう。
外れ値の処理
UMAPを適用する前に、外れ値(異常値)の処理も重要です。
外れ値は他のデータ点と大きく異なる値を持つため、UMAPの距離計算に大きな影響を与える可能性があります。外れ値を適切に処理しないと、次元削減後のデータが歪み、クラスタリングやパターン認識が不正確になることがあるでしょう。
外れ値を処理しない場合、UMAPが外れ値に引きずられ、次元削減結果が正確でなくなる可能性があります。特に、外れ値が局所的な構造に与える影響が大きくなるため、データのクラスターやパターンが歪んでしまうことも。
適切に外れ値を処理することで、UMAPの結果がより信頼性の高いものになります。
標準化・正規化する
UMAPを適用する前に、データの標準化や正規化を行うことは、次元削減の結果に大きな影響を与えます。
UMAPは距離に基づく手法であり、特徴量のスケールが異なると、スケールの大きな特徴量がUMAPの距離計算に強い影響を与え、不正確な結果を生む可能性があるでしょう。
UMAPを適用する際は、事前に標準化や正規化を行うことが推奨されます。標準化や正規化を行わないと、UMAPがスケールの大きな特徴量に偏って学習し、次元削減後の結果が歪む可能性があるでしょう。
標準化や正規化を適切に行うことで、UMAPはデータ全体の構造をより正確に捉え、より意味のある低次元表現が得られます。
UMAPのハイパーパラメータ

UMAPを利用するためには、カテゴリデータや欠損値など、事前に処理が必要なパラメータがあることがわかりました。次に、UMAPのハイパーパラメータには、どのようなパラメータがあるかみていきましょう。
ここでは、以下の項目に分けて、UMAPのハイパーパラメータを解説します。
- n_neighbors
- min_dist
- n_components
これらのパラメータは、UMAPを利用する際にどれも重要なパラメータです。それぞれのパラメータの意味を理解して、適切な値を設定をした上でUMAPを利用するようにしましょう。
n_neighbors
UMAPのハイパーパラメータn_neighborsは、次元削減時にデータポイント間の局所的な構造をどれだけ考慮するかを決定する重要なパラメータです。
このパラメータは、各データポイントの近くにある「隣接する」ポイント数を指定し、局所的な距離の計算に影響を与えます。
n_neighborsの値を小さくすると(例: 5~15)、データの小規模なグループがはっきりと分かれ、より詳細なクラスタリング結果が得られる場合がありますが、全体の構造が無視されることもあるでしょう。
逆に、n_neighborsの値を大きくすると(例: 50~100)、よりグローバルな構造を捉える傾向が強くなり、大きなクラスターや全体的なパターンが浮かび上がりますが、細かい構造が見えにくくなる可能性があります。
min_dist
UMAPのハイパーパラメータmin_distは、次元削減後のデータポイント間の最小距離を制御する重要なパラメータです。
このパラメータは、UMAPがデータの局所的な密度をどれだけ保持するかに影響を与え、低次元空間でのデータの「圧縮度」を決定します。
min_distの値を小さくすると(例: 0.01)、データポイントが密接に配置され、クラスタ内のデータが非常に近くにまとまる結果に。
逆に、min_distの値を大きくすると(例: 0.5~0.99)、ポイント間の距離が広がり、データ全体が均等に広がるようになります。
n_components
UMAPのハイパーパラメータn_componentsは、次元削減後のデータを何次元に投影するかを指定するパラメータです。
UMAPはデータを通常2次元や3次元に可視化することが多いですが、このパラメータによって、次元削減後の空間が決まります。
n_componentsを2に設定すると、データの2次元空間への投影が可能です。2次元は可視化が容易であり、UMAPによる次元削減結果を視覚的に確認しやすく、データのクラスタリングやパターンを直感的に把握できます。
ただし、高次元のデータ構造を単純化するため、一部の情報が失われることがあるでしょう。
n_componentsを3に設定すると、データの3次元空間への投影が可能です。3次元では、より多くの情報を保持した次元削減が可能となり、複雑なデータのパターンを把握する際に役立ちますが、3Dプロットは2Dに比べて視覚的に理解しにくい場合があります。
UMAPの性能評価とベンチマーク

UMAPには、さまざまなハイパーパラメータがあり、それぞれ重要な意味を持つことがわかりました。次に、UMAPの性能評価とベンチマークをみていきましょう。
ここでは、以下の項目に分けて、UMAPの性能評価とベンチマークを解説します。
- 評価指標の選択
- データセットサイズによる性能変化
- 計算時間とメモリ使用量
- 実際のケーススタディ
UMAPの性能評価のためには、評価指標の選択や計算時間とメモリ使用量などのパラメータが重要となります。
評価指標の選択
UMAPの性能評価では、次元削減の結果が元のデータの構造をどれだけ忠実に反映しているかを測ることが重要です。
評価指標の選択は、データの特性や目的に応じて異なりますが、まず、クラスタリング性能が重要な指標となるでしょう。
次元削減後のデータに対してK-meansやDBSCANなどのクラスタリング手法を適用し、その結果の一貫性や分離度を評価することで、UMAPの効果を測定します。
また、視覚的評価も不可欠です。2Dまたは3Dで可視化した結果を専門家が観察し、データの分布やパターンを直感的に把握することができます。
さらに、局所構造の保持度を評価するために、元の高次元データに対するUMAPの結果を比較し、k近傍法や相対距離を利用することが効果的です。
ほかにも、再構成誤差を測定することで、UMAPがどれだけ元の情報を保持しているかを定量的に評価できるでしょう。
データセットサイズによる性能変化
UMAPの性能は、データセットのサイズによって大きく変化します。
小規模なデータセットでは、UMAPは比較的迅速に次元削減を行い、精度も高く、クラスタリングの明瞭さを保ちやすいです。
しかし、データセットが大きくなると、計算コストが増加し、UMAPの処理時間が延びることがあります。特に、n_neighborsやmin_distなどのハイパーパラメータを適切に調整しないと、クラスタリングの精度が低下することがあるでしょう。
また、大規模なデータセットでは、局所的な構造が複雑になり、UMAPが適切にその構造を捉えるためには、より多くのデータポイントを考慮する必要があります。
データのスケールや密度に応じたパラメータ調整が求められ、適切な調整がなされない場合、次元削減の結果が望ましいものにならないことがあるため注意が必要です。
計算時間とメモリ使用量
UMAPの性能評価において、計算時間とメモリ使用量は重要な要素です。
UMAPは高次元データを効率的に次元削減する手法ですが、データセットのサイズや複雑さによって計算コストが大きく変動します。
小規模なデータセットでは、UMAPは迅速に処理を行い、結果を得るのにかかる時間が短くなる傾向に。しかし、大規模なデータセットでは、計算時間が急激に増加し、特にn_neighborsやmin_distなどのハイパーパラメータを設定する際には、メモリ使用量も増加します。
メモリが不足すると、処理が遅延したり、最悪の場合にはクラッシュすることもあるでしょう。メモリ不足とならないように、データの前処理やサンプリングを行い、適切なサイズに調整することが求められます。
また、UMAPの実装によっては、計算効率を改善するためのオプションやパラメータ設定が用意されているため、これらを活用することで、計算時間やメモリ使用量を最適化することが可能です。
実際のケーススタディ
次に、実際のケーススタディをみていきましょう。
バイオインフォマティクス分野では、UMAPを使用して遺伝子発現データを可視化し、細胞タイプのクラスタリングを行うことが一般的です。
また、画像データの処理にもUMAPが活用されています。
さらに、マーケティングデータの分析でもUMAPが利用され、顧客セグメンテーションにおいて、異なる顧客グループを明確に識別するために役立っています。
UMAPと他の次元削減手法との比較

UMAPはさまざまなパラメータで性能評価できることがわかりました。次に、他の次元削減手法との比較をみていきましょう。
以下は、他の次元削減手法である、「t-SNE」と「PCA」をUMAPと比較した一覧表です。
| 手法 | 特徴 | メリット | デメリット |
| UMAP |
|
|
|
| t-SNE |
|
|
|
| PCA |
|
|
|
ここでは、以下の項目に分けて、「t-SNE」と「PCA」をそれぞれ解説します。
- t-SNE
- PCA
それぞれの項目を見ながら、UMAPとの違いを理解し、どちらを利用するのがよいか検討してみてください。
t-SNE
UMAPとt-SNEは、どちらも高次元データを低次元に効果的に可視化するための非線形次元削減手法ですが、いくつかの重要な違いがあります。
t-SNEは、局所的な構造を強調することに特化しており、データのクラスタリングを視覚的に明確にするのが得意です。しかし、計算コストが高く、大規模データセットでは処理が遅くなる傾向があります。
一方、UMAPは、局所構造とグローバルなデータの関係の両方を考慮することができ、高速な計算を実現が可能です。UMAPは、特に大規模なデータセットに対してスケーラビリティがあり、計算時間が短縮される利点があります。
ただし、UMAPはハイパーパラメータの設定が必要で、その調整によって結果が大きく変わることがデメリット。
総じて、UMAPは速度と再現性の面で優れた選択肢となることが多いですが、t-SNEは視覚的なクラスタリングにおいて強力な手法といえるでしょう。
PCA
UMAPとPCA(主成分分析)は、次元削減手法として広く利用されていますが、アプローチや特性に大きな違いがあります。
PCAは線形手法であり、データの分散を最大化する方向に基づいて次元を削減するのが特徴的。計算が非常に速く、解釈も容易ですが、データの非線形構造を捉えることができません。
このため、複雑なデータセットでは重要な情報が失われることも。
一方、UMAPは非線形手法で、局所的なデータの構造を保持しながら次元を削減します。複雑なデータのパターンやクラスタリングを効果的に可視化することが可能です。
UMAPは計算速度も速く、大規模データセットにも適していますが、ハイパーパラメータの調整が必要で、設定によって結果が大きく変わることがデメリット。
総じて、PCAはシンプルで速い方法ですが、UMAPはより複雑なデータの理解を助ける柔軟性を持っています。
UMAPの注意点

UMAP以外にもt-SNE PCAなどの次元削減手法があることがわかりました。次に、UMAPの注意点をみていきましょう。
ここでは、以下の項目に分けて、UMAPの注意点を解説します。
- 日本語データなど数値ではないデータの処理には限界がある
- 再現性の問題
- 解釈の難しさ
UMAPは万能ですが、気をつけなければならない点が幾つがあります。これら注意点に気をつけながら、UMAPを利用しましょう。
日本語データなど数値ではないデータの処理には限界がある
UMAPは主に数値データに最適化された次元削減手法ですが、日本語データやその他の非数値データに対しては限界があります。
対策として、まずテキストデータをベクトル化するために、TF-IDFやWord2Vec、BERTなどの手法を使用することが考えられます。これらの手法を用いれば、テキストの意味を保持したまま数値データに変換が可能です。
さらに、カテゴリデータについては、One-Hotエンコーディングやラベルエンコーディングを用いて数値化し、UMAPに適用することができます。
ただし、ベクトル化の手法によって結果が異なるため、データの特性に適した方法を選択することが重要です。適切な前処理を行うことで、UMAPを効果的に活用し、非数値データの次元削減を実現できます。
再現性の問題
UMAPは高次元データの次元削減に優れた手法ですが、再現性の問題がある点に注意が必要です。
UMAPは初期化の際にランダムな要素を含むため、同じデータに対しても実行するたびに異なる結果が得られることがあります。特に比較研究や実験においては、結果の再現性が課題となることがあるでしょう。
この再現性の問題に対する対策として、まずランダムシードを固定することが挙げられます。UMAPの実行時にrandom_stateパラメータを指定することで、初期化のランダム性を制御し、同じ結果を再現しやすくすることが可能。
また、UMAPの結果を評価する際には、複数の実行結果を統計的に比較し、結果のばらつきを考慮することが重要です。
さらに、結果を保存し、詳細なプロセスを文書化することで、後の再現性を確保する助けにもなります。
解釈の難しさ
UMAPは高次元データの次元削減において強力な手法ですが、結果の解釈が難しい点に注意です。
UMAPは非線形手法であるため、低次元に圧縮されたデータの背後にある高次元の構造を直感的に理解するのが難しく、クラスタの意味やデータ間の距離の解釈に困難をともないます。得られた可視化結果が実際のデータの特性を正確に反映しているか疑問が生じることがあるでしょう。
この解釈の難しさに対する対策として、まず結果を他の手法(例えばPCAやt-SNE)と併用して比較することが有効です。異なる手法から得られた可視化結果を相互に照らし合わせることで、データの特徴をより深く理解できます。
また、データの専門知識を持つ人と協力し、クラスタの意味やデータの特性についての議論を行うことも重要です。
さらに、UMAPのハイパーパラメータ(例:n_neighborsやmin_dist)を適切に調整し、結果の変化を観察することで、可視化結果の安定性を確保することができます。
UMAPのまとめ

今回は、UMAPに関して、以下のことがわかりました。
- UMAPは高次元データの次元を低次元に削減する手法の一つ
- UMAPを活用すればパターンやクラスターが視覚的に確認しやすくなる
- 異常検知や音声認識などにUMAPの活用例がある
- 評価指標の選択がUMAPを評価する上で重要
UMAPは、高次元データを低次元に削減する手法の一つですが、どのように活用してよいかわからないこともあるでしょう。
UMAPに関して不明点やわからないことがあれば、AI開発に多くの知見を持つ、株式会社Jiteraにご相談ください。自社にて、UMAPをどのように活用したいかをヒアリングさせていただき、最適なアドバイスを差し上げます。